Euler's sum of powers conjecture
Euler's conjecture is a disproved conjecture in mathematics related to Fermat's last theorem which was proposed by Leonhard Euler in 1769. It states that for all integers n and k greater than 1, if the sum of n kth powers of positive integers is itself a kth power, then n is greater than or equal to k.
In symbols, if 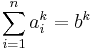 where
where 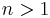 and
and  are positive integers, then
are positive integers, then 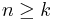 .
.
If the conjecture were true, it would be a generalization of Fermat's last theorem, which could be seen as the special case n = 2: if 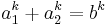 , then
, then 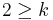 .
.
Contents |
Counterexamples
k = 5
The conjecture was disproven by L. J. Lander and T. R. Parkin in 1966 when they found the following counterexample for k = 5:
-
- 275 + 845 + 1105 + 1335 = 1445.
Yet another counterexample 852825 + 289695 + 31835 + 555 = 853595 was found by Jim Frye in 2004.
k = 4
In 1986, Noam Elkies found a method to construct counterexamples for the k = 4 case.[1] His smallest counterexample was the following:
-
- 26824404 + 153656394 + 187967604 = 206156734.
A particular case of Elkies' solution can be reduced to the identity,[2][3]
-
- (85v2+484v−313)4 + (68v2−586v+10)4 + (2u)4 = (357v2−204v+363)4
where
-
- u2 = 22030+28849v−56158v2+36941v3−31790v4.
This is an elliptic curve with one solution as v1 = −31/467. From this initial rational point, one can then compute an infinite number of vi. Substituting v1 into the identity and removing common factors gives the numerical example cited above.
In 1988, Roger Frye subsequently found the smallest possible k = 4 counterexample by a direct computer search using techniques suggested by Elkies:
-
- 958004 + 2175194 + 4145604 = 4224814.
Moreover, this solution is the only one with values of the variables below 1,000,000.
Generalizations
In 1966, L. J. Lander, T. R. Parkin, and John Selfridge conjectured that if 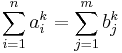 , where ai ≠ bj are positive integers for all 1 ≤ i ≤ n and 1 ≤ j ≤ m, then m+n ≥ k. This would imply as a special case that if
, where ai ≠ bj are positive integers for all 1 ≤ i ≤ n and 1 ≤ j ≤ m, then m+n ≥ k. This would imply as a special case that if
(under the conditions given above) then n ≥ k−1.
See also
References
- ^ Noam Elkies (1988). "On A4 + B4 + C4 = D4". Mathematics of Computation 51 (184): 825–835. doi:10.2307/2008781. JSTOR 2008781. MR0930224.
- ^ "Elkies' a^4+b^4+c^4 = d^4". http://groups.google.com/group/sci.math/browse_thread/thread/15beef75eaddcb1b?hl=en#.
- ^ "Sums of Three Fourth Powers". http://sites.google.com/site/tpiezas/014.
External links
- A Collection of Algebraic Identities
- EulerNet: Computing Minimal Equal Sums Of Like Powers
- J. Wroblewski Equal Sums of Like Powers
- Weisstein, Eric W., "Euler's Sum of Powers Conjecture" from MathWorld.
- Weisstein, Eric W., "Euler Quartic Conjecture" from MathWorld.
- Weisstein, Eric W., "Diophantine Equation--4th Powers" from MathWorld.
- Euler's Conjecture at library.thinkquest.org
- A simple explanation of Euler's Conjecture at Maths Is Good For You!
- Mathematicians Find New Solutions To An Ancient Puzzle
- Ed Pegg Jr. Power Sums, Math Games